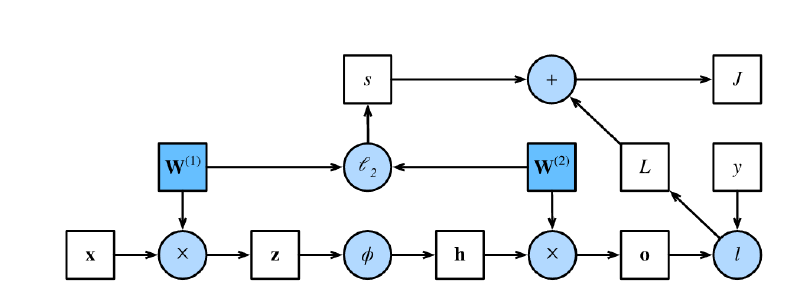
前向传播
前向传播(forward propagation):按顺序(输入层$\to$输出层)计算和存储神经网络中每层的结果。
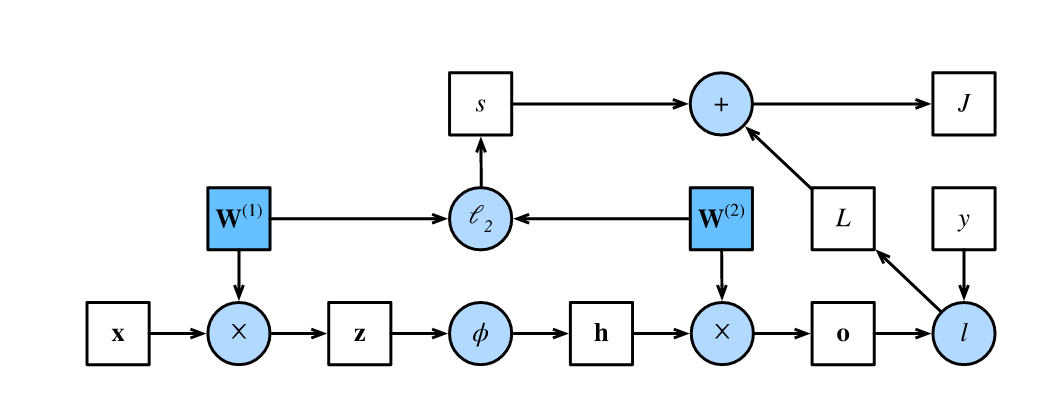
讨论示例: 预设:隐藏层不包括偏置项
- 输入样本$\mathbf{x}\in \mathbb{R}^d$
- 隐藏层的权重参数$\mathbf{W}^{(1)} \in \mathbb{R}^{h \times d}$
- 中间变量$\mathbf{z}= \mathbf{W}^{(1)} \mathbf{x}$
- $\mathbf{z}\in \mathbb{R}^h$
- 激活函数$\phi$
- 隐藏激活向量$\mathbf{h}= \phi (\mathbf{z})$
- $\mathbf{h}\in \mathbb{R}^h$
- 输出层的权重参数$\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$
- 输出层变量$\mathbf{o}= \mathbf{W}^{(2)} \mathbf{h}$
- $\mathbf{o}\in \mathbb{R}^q$
- 单个数据样本的损失项$L = l(\mathbf{o}, y)$
- 损失函数$l$
- 样本标签$y$
- 正则化项$s = \frac{\lambda}{2} \left(\|\mathbf{W}^{(1)}\|_F^2 + \|\mathbf{W}^{(2)}\|_F^2\right)$
- $L_2$正则化
- 超参数$\lambda$
- 模型在给定数据样本上的正则化损失$J = L + s$
- 即此时的目标函数(objective function)。
- 正方形表示变量,圆圈表示操作符。
- 左下角表示输入,右上角表示输出。
- 箭头显示数据流的方向,主要是向右和向上。
反向传播
反向传播(backward propagation):计算神经网络参数梯度的方法。 根据微积分中的链式法则,按相反的顺序从输出层到输入层遍历网络。
- 存储计算某些参数梯度时所需的任何中间变量(偏导数)
- $\text{prod}$运算符:在执行必要的操作(如换位和交换输入位置)后将其参数相乘。
- 目的:计算梯度$\frac{\partial J}{\partial \mathbf{W}^{(1)}}$和$\frac{\partial J}{\partial \mathbf{W}^{(2)}}$
- 先计算距离输出层更近的$\frac{\partial J}{\partial \mathbf{W}^{(2)}}$
由于$\frac{\partial J}{\partial L}=1$,故$\frac{\partial L}{\partial \mathbf{h}}$在数值上等于$\frac{\partial J}{\partial \mathbf{h}}$,下述$\frac{\partial J}{\partial \mathbf{h}}$、$\frac{\partial J}{\partial \mathbf{z}}$按此对应上述推导。
激活函数$\phi$是按元素计算的,计算中间变量$\mathbf{z}$的梯度$\frac{\partial J}{\partial \mathbf{z}} \in \mathbb{R}^h$ 需要使用按元素乘法运算符,用$\odot$表示:
$$ \frac{\partial J}{\partial \mathbf{z}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{h}}, \frac{\partial \mathbf{h}}{\partial \mathbf{z}}\right) = \frac{\partial J}{\partial \mathbf{h}} \odot \phi'\left(\mathbf{z}\right) $$隐藏层输出的梯度$\frac{\partial J}{\partial \mathbf{h}} \in \mathbb{R}^h$由下式给出:
$$ \frac{\partial J}{\partial \mathbf{h}} = \text{prod}\left(\frac{\partial J}{\partial \mathbf{o}}, \frac{\partial \mathbf{o}}{\partial \mathbf{h}}\right) = {\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}} $$$J$ 是一个标量(损失函数的输出),$\mathbf{o}$ 是 $q$ 维向量,按照多元微积分,$\frac{\partial J}{\partial \mathbf{o}}$形状和 $\mathbf{o}$ 一致,即 $\frac{\partial J}{\partial \mathbf{o}} \in \mathbb{R}^q$;又$\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$,故:
$$ {{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}} \in \mathbb{R}^h $$${{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}}$与${\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)}}$
在反向传播的推导中,更常用${{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}}$ 的写法,主要考虑以下:
- 链式法则 通过上一层的梯度左乘该层权重的转置,得到每一层的梯度
- 与前向传播的结构对偶
- 前向传播:$\mathbf{o} = \mathbf{W}^{(2)} \mathbf{h}$
- 反向传播:$\frac{\partial J}{\partial \mathbf{h}} = {\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}$
对于$\mathbf{W}^{(2)} \in \mathbb{R}^{q \times h}$,为了在计算$\frac{\partial J}{\partial \mathbf{h}}$时形状匹配:
- $\frac{\partial J}{\partial \mathbf{h}} = {{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}}$:应将$\frac{\partial J}{\partial \mathbf{o}}$ 视作是 $q \times 1$ 的列向量($\mathbb{R}^{q \times 1}$),得到$\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)} \in \mathbb{R}^{h \times 1}$
- $\frac{\partial J}{\partial \mathbf{h}} = {\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)}}$:应将$\frac{\partial J}{\partial \mathbf{o}}$ 视作是 $1 \times q$ 的行向量($\mathbb{R}^{1 \times q}$),得到$\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)} \in \mathbb{R}^{1 \times h}$
区分行/列向量,不是改变变量的本质维度,是为了在矩阵乘法等操作时形状能严格对齐。
但在具体的编程实现时,${{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}}$与${\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)}}$很可能一致。
对于表述$\frac{\partial J}{\partial \mathbf{o}} \in \mathbb{R}^q$,只表示“$q$ 维实向量”,不区分是行向量还是列向量,也不强调是1维还是2维(抽象意义上是1维向量);而例如$\frac{\partial J}{\partial \mathbf{o}} \in \mathbb{R}^{q \times 1}$则明确表示“$q$ 行 $1$ 列的矩阵”,也就是列向量,在数学和编程实现中是2维的。
在实际编程(如 NumPy、PyTorch)中,
- $\mathbb{R}^q$ 通常对应 shape 为
(q,)的一维数组(向量) - $\mathbb{R}^{q \times 1}$ 对应 shape 为
(q, 1)的二维数组(列向量) - $\mathbb{R}^{1 \times q}$ 对应 shape 为
(1, q)的二维数组(行向量)
$\frac{\partial J}{\partial \mathbf{o}}$ 的 shape 取决于你的实现方式和数据批量:
单样本(无batch):
- $\mathbf{o}$ 是 $q$ 维向量,通常 shape 为
(q,)(一维数组),也可能是(q, 1)(二维列向量) - 此时,$\frac{\partial J}{\partial \mathbf{o}}$ 的 shape 通常为
(q,)或(q, 1)
- $\mathbf{o}$ 是 $q$ 维向量,通常 shape 为
批量(batch):
- $\mathbf{o}$ 是 shape
(batch_size, q),即每一行对应一个样本的输出 - 此时,$\frac{\partial J}{\partial \mathbf{o}}$ 的 shape 为
(batch_size, q)
- $\mathbf{o}$ 是 shape
多数情况我们会使用batch,借助PyTorch 的 @ 运算(也即matmul),自动对第一个维度(batch 维)进行广播和批量矩阵乘法。此时,不论是通过${{\mathbf{W}^{(2)}}^\top \frac{\partial J}{\partial \mathbf{o}}}$还是通过${\frac{\partial J}{\partial \mathbf{o}} \cdot \mathbf{W}^{(2)}}$,均使用dJ_dh = dJ_do @ W2语句得到$\frac{\partial J}{\partial \mathbf{h}}$。
内存开销
反向传播重复利用前向传播中存储的中间值,以避免重复计算。影响之一是需要保留中间值,直到反向传播完成。这也是训练比单纯的预测需要更多的内存(显存)的原因之一。 此外,这些中间值的大小与网络层的数量和批量的大小大致成正比,因此,使用更大的批量来训练更深层次的网络更容易导致内存不足(out of memory)。